
Do you feel that you’ve written all you could in this essay, but it’s still short of the word count requirement? Maybe you need to add a few hundred or even a thousand words.
If so, you’ve come to the right place. I’m Tutor Phil, and in this tutorial I’ll show you how to increase your essay’s word count.
These four tips or techniques will work for any type of an essay. They will also improve the quality of your paper.
So, let’s dive right in. Here are…
Four easy ways to expand your essay:
1. Add an explanation
If you read through your essay, you will likely notice that one or more ideas could use some kind of an explanation.
Very often, we assume that the reader is familiar with all the concepts that we discuss in our writing. But what if we could find a concept or a term that many people might actually be unfamiliar with?
That’s our opportunity to expand our paper. Here’s an example. Let’s assume you’re writing an essay on human psychology, and you include this statement:
“John became a victim of the ostrich effect when he chose to deny that his family did not share his outlook on the situation.”
One phrase stands out in this sentence. Some readers may wonder: “What is an ‘ostrich effect?’”
If they are unfamiliar with the term, they might need to distract themselves from your essay for a second and go look it up.
What if you did the work for them and simply explained the term in your essay:
“The ‘ostrich effect’ refers to a peculiar behavior of this tropical bird in dangerous or critical situations. When facing danger, an ostrich buries its head in the sand. This way, it prevents itself from seeing what is happening around it. Unfortunately, while this helps relieve anxiety, this is not an effective strategy to deal with the actual threat.”
By adding this explanation, we just added 58 words to the essay. And we can probably find another concept or two to explain.
This is especially effective when you’re writing an essay on some complex topic. But it can work in a simple and mundane topic, as well. You can even deliberately plant an uncommon concept and then explain it.
How to use this technique
To use this technique over and over in your essay, all you need to do is read through the body of your essay from the beginning, scanning it for a term that may be unfamiliar to the reader.
Here are some questions you can ask and then provide an answer as an explanation.
What is this?
The answer to this question defines something. It is usually a short description of the idea or a thing.
How does this work?
This question gives you a chance to add quite a bit of content. In it, you would explain or describe how something works, from beginning to end.
If it’s some kind of a mechanical contraption, you can describe its components, explain what each one does, and describe the entire process of its function.
If it’s a natural process, such as the development of a fetus, you can describe that process in some detail.
You can do the same with a computer program or app, a legal procedure, or anything else that consists of parts and takes steps or stages to complete.
Why is it effective?
Here is your chance to explain why this thing or process works well. In effect, you are describing the strengths and advantages of the thing or process.
What does it enable?
By answering this question, you explain what other things, effects, or benefits become possible thanks to the thing or process you’re discussing.
Note that you can use any and all of these questions for every concept you want to expand on.
But use your discretion. This technique is very powerful, and it’s easy to go overboard and explain too much.
Remember – you have three other techniques you can use. So, employ a variety of these methods.
2. Use the Counterargument technique
Here is a very effective technique to add two paragraphs of quality material to your paper. You can use this technique multiple times in your essay while making your argumentation more powerful.
I call it the Counterargument technique, and it has three easy steps.
The Counterargument Technique
Step 1. Pick a spot in your paper where one of the authors you’ve used as a source could disagree with a point.
This should not be your main point. Choose a supporting idea in the body of your essay that sounds like someone could challenge it.
Let’s use an example of a paper on human psychology again, and let’s say that one of the points you make is that people almost never change. This statement sounds like someone out there could challenge it.
Once we’ve picked the statement, we’re ready for the next step.
Step 2. Challenge this statement.
You can introduce your challenge in one of the following ways:
“Some authors disagree with this assumption. They claim that…”
“Some may argue that…”
And then you explain what they claim.
This could be an author that you have already researched. Or, you could go out there and find just one article in which the author presents an argument contrary to the statement you chose.
Don’t worry – the whole source doesn’t have to challenge the statement. If only a small part of it contains contradictory material, you have just found your challenge. And now you’re ready for the next step.
Step 3. Answer the challenge.
In this step, you simply write down an answer or a rebuttal to the challenge you just presented. When you do this, you provide even stronger support for your thesis.
For example, it can go something like this:
The original argument:
“People almost never change.”
The challenge:
“Well, some authors seem to disagree with this view and claim that people can change under certain circumstances.”
And here you can cite this other author or authors who present the challenge.
And now comes the answer to the challenge:
“However, these authors are mistaken because modern psychology presents abundant evidence that human psychology loves the status quo.”
And you can provide the reason or reasons you believe the challenge does not hold water. You can make your counterargument as detailed as you want and even add examples.
When you do it the way I just described, you are not contradicting yourself.
Instead, you are actually strengthening your argument because you show that you are aware that some people may disagree with it. But their argument is weak for the reasons that you provide.
Here’s a video I created to walk you through this technique:
3. Add examples
I have graded a lot of papers as a university writing instructor. And I can tell you that students don’t use enough examples in their essays.
Their content is mostly general. Sometimes, they’ll use statistics or formal facts. But those are not specific examples.
An example is usually an image or a story, a depiction of an event or a description of a human being in a particular place and time.
Examples have colors, smells, names, exact dates, and other details that make them come alive in the reader’s imagination.
Let’s come back to our imaginary essay about human psychology in which John is used as a general example of the “ostrich effect.”
We wrote a nice explanation of the effect earlier. But we don’t have to leave it at that. We can now add a specific example of John being a victim of the ostrich effect:
“For the past three weeks, John’s wife Liz has tried to get him to recognize that their daughter had been receiving poor grades in school. But faced with the challenges of his new business, John has just kept brushing the topic aside. One day Liz became so angry with her husband that she simply stopped talking to him. That got his attention.”
This is a specific example of John’s habit of denying important facts. We can extend this example even more by providing more details.
The beauty of using examples is that you can write as much or as little as you want without struggling for words.
Here’s a tip: you can use your personal examples. And you can include them in simple essays that you would write on a test or even in research papers.
Just make sure that your personal example is relevant and serves to support the point.
4. Add a whole section
This technique is great for expanding your essay by a lot – by 30% or more. And you can even repeat it and add more than one whole section.
Let’s say that you have three supporting ideas for your main point. And you have already written as much as you could about those three points.
To use our human psychology example, let’s say that this is our main structure:
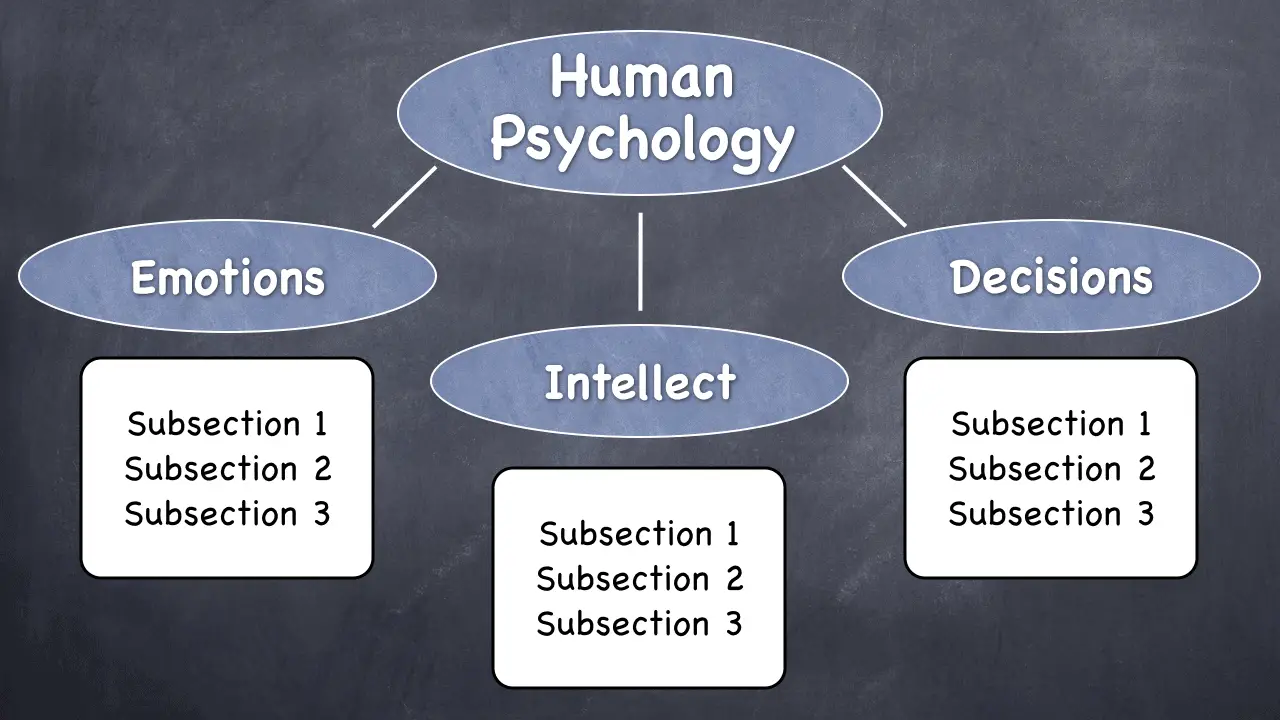
We have three nice sections, each devoted to a part of human psychology. And let’s say that our thesis is the following:
“The three parts of human psychology that primarily determine behavior are emotions, intellect, and decision-making.”
And let’s say that each section in this paper is about 500 words long. And we need another 500 words.
Can we think of another part of human psychology that also determines human behavior? Of course we can.
I’ll just consult my own basic knowledge of psychology to do it. You can consult your own knowledge or do quick research to find one more supporting idea.
And here we are. The ego is another major contributor to human behavior.
Now, let’s add this to our whole structure:
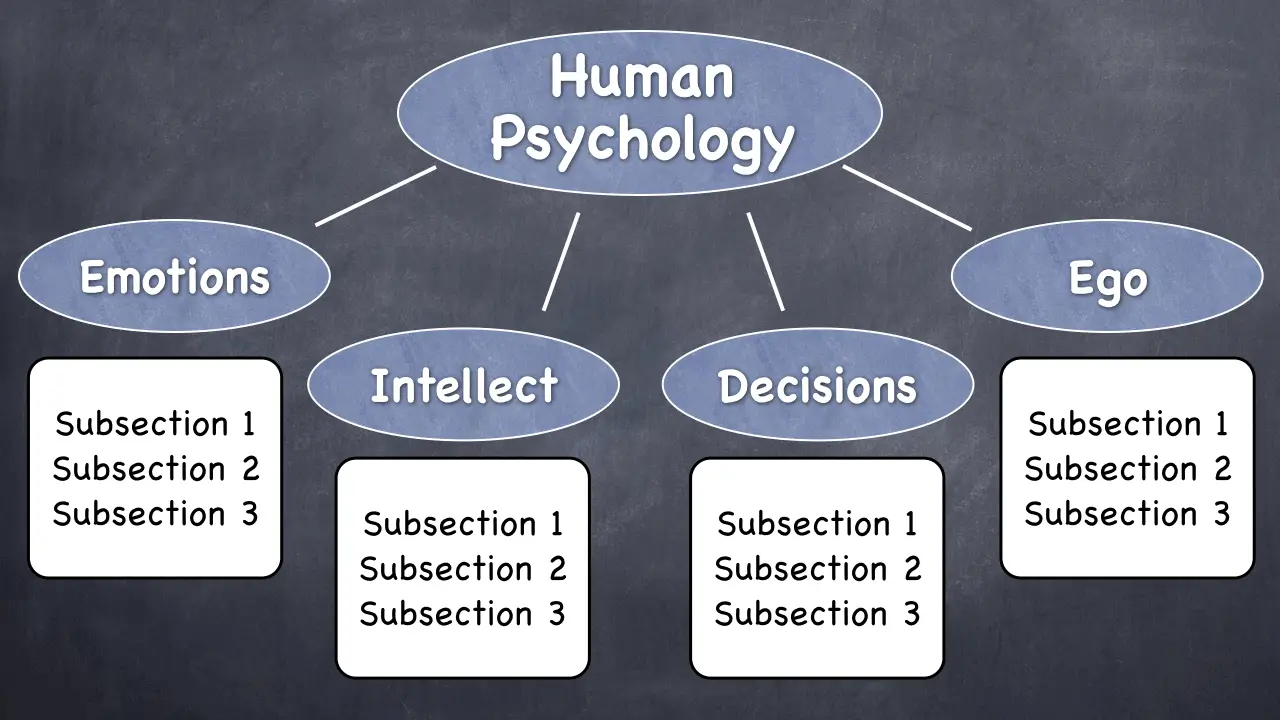
Given that this section is similar in length to the others, by the time we have written it out in the body of the essay, we’ll have 500 more words!
Also, we must not forget to update our thesis statement:
“The four parts of human psychology that primarily determine behavior are emotions, intellect, decision-making, and the ego.”
If you wonder how to fill out a new section with high quality material, you should read my guide on how to write body paragraphs.
Hope this is helpful!
Tutor Phil
